


 |
 |
 |
This first part introduces the reference system I have chosen to make an analysis of tonality.
When there is no musical context more complex, the key is determined by the perfect cadence, in which the tonic (or keytone) follows the dominant (that is, the tonic's fifth). (The dominant → tonic succession can be abbreviated as V → I.) Here is an example:
The perfect cadence is often preceded by the subdominant (that is, the tonic's fourth). It is the full cadence, abbreviated as IV → V → I. Here is an example:
Once the key is determined, the major or minor mode is determined by the mediant (that is, the tonic's major or minor third, abbreviated as III) contained in the musical phrase. Here is an example of a major key and mode:
Here is an example of a minor key and mode:
These initial considerations, present in a number of treatises on musical theory, suffer from an important deficit of logic. Talking of tonic, mediant, dominant, subdominant, or degrees I, III, IV, or V assumes we have already determined the key, whereas the intention here is to determine it.
In the previous examples, we simply hear intervals between pitches. Moreover, it does not matter whether the intervals are melodic (that is, between successive notes) or harmonic (that is, between notes of a chord). Thanks to our auditory memory, our ears make a synthesis of the sounds and of the melodic or harmonic intervals they hear.
It does not matter, either, that the pitches are approximate because, as explained in reconciling tuning systems, our ears, in search of consonance, mostly hear what they want to hear.
In this initial approach to tonality, it does not matter whether intervals are ascending or descending. (In the first example, the interval of ascending fourth is well worth the interval of descending fifth of the second example. Both determine the same C key.) It does not matter, either, whether or not the intervals are contained within the extent of an octave.
Assuming a key is determined, we can write the notes on a musical staff, choosing the key signature (that is, the sharps or flats of the piece or of the musical phrase) according to the key thus determined.
Using a key signature especially fits the major mode, because we can represent all notes of a major key with no special alteration (sharp, flat, natural, etc.).
It less fits the minor mode because, in the minor mode, degrees VI and VII are quite varying. Because degrees VI and VII of a minor key require varying alterations, it is customary to use the key signature of the relative major key (for example, we note A minor using the key of C major). Using an approximate key signature for the minor mode leads, when necessary, to raising degrees VI or VII by a semitone (or half step), making certain alterations (sharps or naturals) mandatory.
The variability of degrees VI and VII makes determining a minor key more complex than doing a major key.
For the few other notes that do not comply with the key signature, the composer chooses some alterations according to more or less strict musical writing standards. Economical writing is always welcome. For example, in the key of C major or A minor, it would not be done to write B sharp or F flat.
As discussed earlier, as long as a key is not determined, writing notes on a staff in no way helps analyze the tonality of a musical phrase. The key determines the key signature, not the other way around.
Because, in this initial approach, the tonal relationships between notes do not depend on the octaves that contain the notes, a circular representation better fits tonality analysis.
The twelve notes of the chromatic scale happen to form what mathematicians call a ring, specifically the Z/12Z ring. Here is a (circular indeed) representation of that ring:
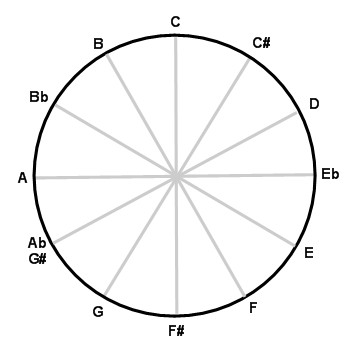
This first representation clearly shows the successive degrees of the chromatic scale, especially the relationships between the leading (or sensible) note (degree VII) and the tonic (degree I) which are close together in this circular representation.
It less well shows the (major or minor) diatonic scale. Let us start analyzing the major scale, in which degrees VI and VII are unvarying.
The major scale is formed by successive fifths (or successive fourths, which is equivalent). Seven fifths (or fourths) form the seven degrees of the major scale. (Continuing beyond seven fifths or fourths would form the chromatic scale, indeed.)
Mathematicians would say that the fifth, fourth, major seventh and minor second are units of our Z/12Z ring. Moreover, mathematicians tell us that there are no other units. In musical terms, it means that the fifth, minor second and their inversions are the only intervals that generate the chromatic scale.
Because the major scale is formed by successive fifths or fourths, a circular representation by the circle of fifths better fits analyzing a key, especially a major key. Here is the second representation of the Z/12Z ring:
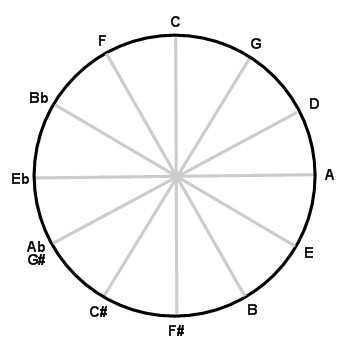
This new representation has the advantage of showing degrees IV, I and V side by side. These intervals, being constitutive of cadences, are the cornerstones of tonality. On the contrary, it has the drawback that the leading note (degree VII) is far from the tonic, in the position diametrically opposite to the subdominant (degree IV).
The balance of advantages and disadvantages being in favor of this second representation, it is the one used in the present analysis of tonality.
Back to the above examples of cadences, let us now represent them on the circle of fifths.
Here is the perfect cadence (V → I):
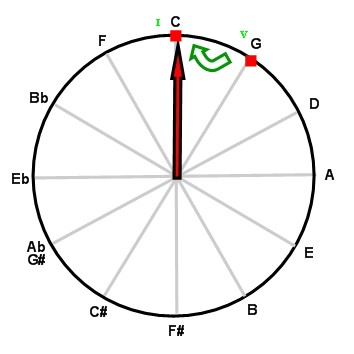
On the circle of fifths, degrees V and I are contiguous. The tonic is the first note encountered, clockwise.
Here is the full cadence (IV → V → I):
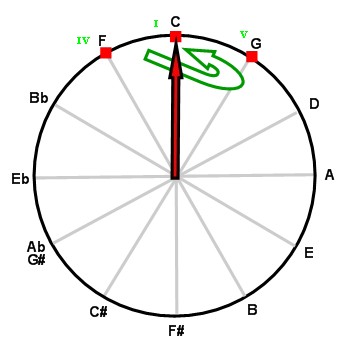
On the circle of fifths, degrees IV, I and V are contiguous. The tonic stands in the central position.
The circle of fifths behaves like a compass in which degrees I, IV and V swing around the tonic. (In the above figures, the needle of our tonal compass designates the tonic.)
The major mode is characterized by its mediant (degree III) which forms a major third with the tonic. The minor mode is characterized by a lower mediant, which forms a minor third with the tonic, and by the variability of degrees VI and VII, too. In both modes, degree II is unvarying. Degrees I through V therefore characterize both the key and the mode.
Here are the relative positions, on the cycle of fifths, of the seven degrees of the major scale:
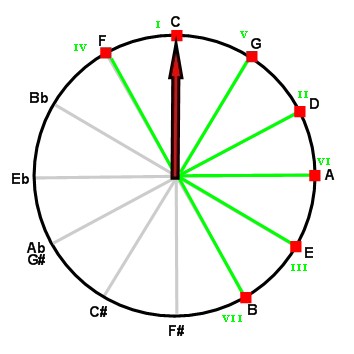
The seven degrees form a semicircle in which the subdominant (degree IV) and the leading note (degree VII) delimit the diameter.
As discussed above, degrees I through V characterize the major mode. Here are their respective positions:
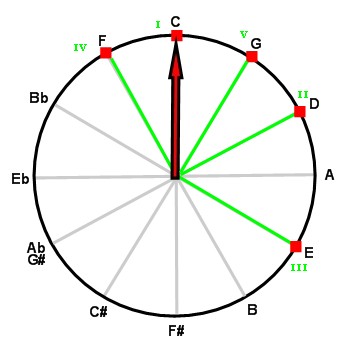
As a matter of fact, the mediant (degree III) alone is enough for us to hear the major mode. When degrees I, III and V (or even I and III, if we have just heard V) form a major chord (or arpeggio) that sounds separately, they are enough to establish the major mode. Here are two C major chords, where the dominant is optional and shown between parentheses (click to listen):
In the second chord, the dominant becomes optional because it has just been heard.
Because degrees VI and VII are varying, there are several minor scales for one minor key. This figure shows the relative positions of the seven degrees of the minor scale on the cycle of fifths, with brown radiuses leading to the degrees that are varying:
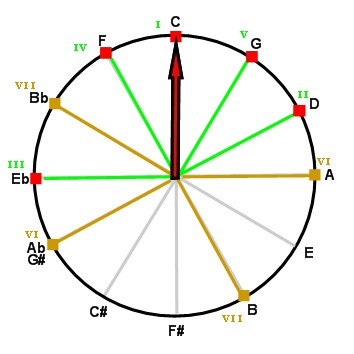
The minor scale includes the seven notes of its relative major key. It also includes two additional degrees raised by one semitone. The similarity between scales explains how composers easily modulate between relative keys. Relative keys are often intertwined in the same theme or the same phrase.
As they do in the major mode, degrees I through V characterize the minor mode. Here are their respective positions:
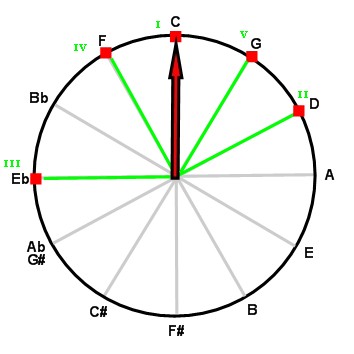
As it does in the major mode, the mediant (degree III) alone is enough for us to hear the minor mode. When degrees I, III and V (or even I and III, if we have just heard V) form a minor chord (or arpeggio) that sounds separately, they are enough to establish the minor mode. Here are two C minor chords, where the dominant is optional and shown between parentheses (click to listen):
In the second chord, as it does in the major mode, the dominant becomes optional because it has just been heard.
|
Jean-Pierre Vial January 2021 |
 |
 |
 |

|